publications
2023
-
Sliding, vibrating and swinging droplets on an oscillating fibreStéphane Poulain, and Andreas CarlsonJournal of Fluid Mechanics, 2023We study experimentally the dynamics of a water droplet on a tilted and vertically oscillating rigid fibre. As we vary the frequency and amplitude of the oscillations the droplet transitions between different modes: harmonic pumping, subharmonic pumping, a combination of rocking and pumping modes, and a combination of pumping and swinging modes. We characterize these responses and report how they affect the sliding speed of the droplet along the fibre. The swinging mode is explained by a minimal model making an analogy between the droplet and a forced elastic pendulum.
2022
-
Droplet settling on solids coated with a soft layerStéphane Poulain, and Andreas CarlsonJournal of Fluid Mechanics, 2022Gravitational settling of a droplet in air onto a soft substrate is a ubiquitous event relevant to many natural processes and engineering applications. We study this phenomenon by developing a three-phase lubrication model of droplet settling onto a solid substrate coated by a thin soft layer represented by a viscous film, an elastic compressible layer and an elastic sheet supported by a viscous film. By combining scaling analysis, analytical methods and numerical simulations we elucidate how the resulting droplet dynamics is affected by the nature of the soft layer. We show that these soft layers can significantly affect the droplet shape during gravitational settling. When there is a linear response of the deformations of the soft layer, the air layer takes longer to drain as compared with the case of a droplet settling onto a rigid substrate. Our results provide new insight into the coupled interactions between droplets and solids coated by a thin film of a soft material.
-
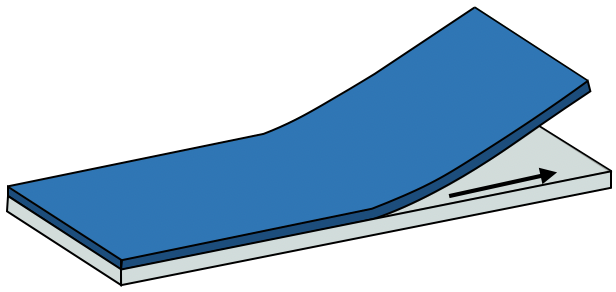Elastohydrodynamics of contact in adherent sheetsStéphane Poulain, Andreas Carlson , Shreyas Mandre , and L MahadevanJournal of Fluid Mechanics, 2022Adhesive contact between a thin elastic sheet and a substrate arises in a range of biological, physical and technological applications. By considering the dynamics of this process that naturally couples fluid flow, long-wavelength elastic deformations and microscopic adhesion, we analyse a sixth-order thin-film equation for the short-time dynamics of the onset of adhesion and the long-time dynamics of a steadily propagating adhesion front. Numerical solutions corroborate scaling laws and asymptotic analyses for the characteristic waiting time for adhesive contact and for the speed of the adhesion front. A similarity analysis of the governing partial differential equation further allows us to determine the shape of a fluid-filled blister ahead of the adhesion front. Finally, our analysis reveals a near-singular behaviour at the moving elastohydrodynamic contact line with an effective boundary condition that might be useful in other related problems.
2019
-
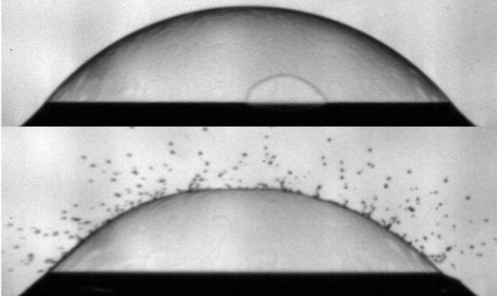Disease transmission via drops and bubblesStéphane Poulain, and Lydia BourouibaPhysics Today, 2019Gravitational settling of a droplet in air onto a soft substrate is a ubiquitous event relevant to many natural processes and engineering applications. We study this phenomenon by developing a three-phase lubrication model of droplet settling onto a solid substrate coated by a thin soft layer represented by a viscous film, an elastic compressible layer and an elastic sheet supported by a viscous film. By combining scaling analysis, analytical methods and numerical simulations we elucidate how the resulting droplet dynamics is affected by the nature of the soft layer. We show that these soft layers can significantly affect the droplet shape during gravitational settling. When there is a linear response of the deformations of the soft layer, the air layer takes longer to drain as compared with the case of a droplet settling onto a rigid substrate. Our results provide new insight into the coupled interactions between droplets and solids coated by a thin film of a soft material.
2018
-
Broadening of cloud droplet size spectra by stochastic condensation: Effects of mean updraft velocity and CCN activationGaetano Sardina , Stéphane Poulain, Luca Brandt , and Rodrigo CaballeroJournal of the Atmospheric Sciences, 2018The authors study the condensational growth of cloud droplets in homogeneous isotropic turbulence by means of a large-eddy simulation (LES) approach. The authors investigate the role of a mean updraft velocity and of the chemical composition of the cloud condensation nuclei (CCN) on droplet growth. The results show that a mean constant updraft velocity superimposed onto a turbulent field reduces the broadening of the droplet size spectra induced by the turbulent fluctuations alone. Extending the authors’ previous results regarding stochastic condensation, the authors introduce a new theoretical estimation of the droplet size spectrum broadening that accounts for this updraft velocity effect. A similar reduction of the spectra broadening is observed when the droplets reach their critical size, which depends on the chemical composition of CCN. The analysis of the square of the droplet radius distribution, proportional to the droplet surface, shows that for large particles the distribution is purely Gaussian, while it becomes strongly non-Gaussian for smaller particles, with the left tail characterized by a peak around the haze activation radius. This kind of distribution can significantly affect the later stages of the droplet growth involving turbulent collisions, since the collision probability kernel depends on the droplet size, implying the need for new specific closure models to capture this effect.
-
Universal rim thickness in unsteady sheet fragmentationYongji Wang , Raj Dandekar , Nicole Bustos , Stéphane Poulain, and Lydia BourouibaPhysical Review Letters, 2018Unsteady fragmentation of a fluid bulk into droplets is important for epidemiology as it governs the transport of pathogens from sneezes and coughs, or from contaminated crops in agriculture. It is also ubiquitous in industrial processes such as paint, coating, and combustion. Unsteady fragmentation is distinct from steady fragmentation on which most theoretical efforts have been focused thus far. We address this gap by studying a canonical unsteady fragmentation process: the breakup from a drop impact on a finite surface where the drop fluid is transferred to a free expanding sheet of time-varying properties and bounded by a rim of time-varying thickness. The continuous rim destabilization selects the final spray droplets, yet this process remains poorly understood. We combine theory with advanced image analysis to study the unsteady rim destabilization. We show that, at all times, the rim thickness is governed by a local instantaneous Bond number equal to unity, defined with the instantaneous, local, unsteady rim acceleration. This criterion is found to be robust and universal for a family of unsteady inviscid fluid sheet fragmentation phenomena, from impacts of drops on various surface geometries to impacts on films. We discuss under which viscous and viscoelastic conditions the criterion continues to govern the unsteady rim thickness.
-
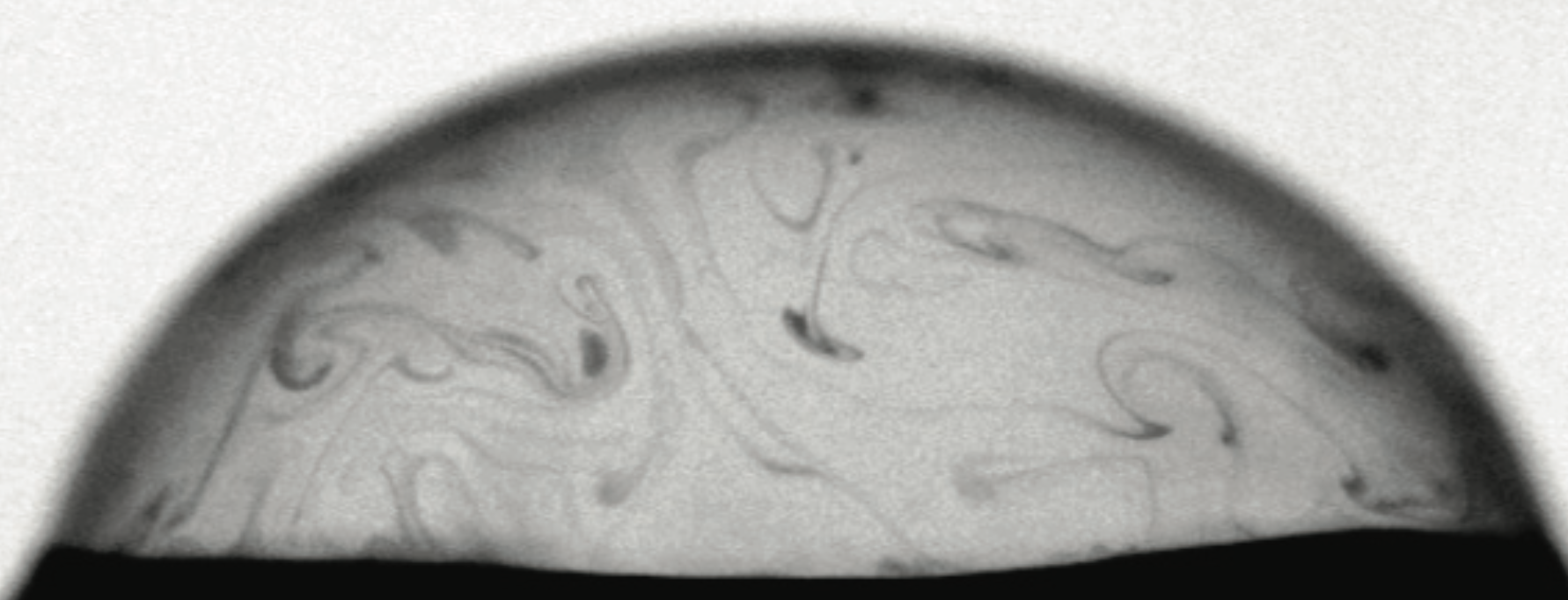Ageing and burst of surface bubblesStéphane Poulain, Emmanuel Villermaux , and Lydia BourouibaJournal of Fluid Mechanics, 2018Upon burst, surface bubbles transfer biological and chemical material from water bodies to the air we breathe via the production of droplets. An understanding of what shapes the size and payload of such droplets starts by understanding the fundamental physics of bubble birth, drainage and burst. Our combined experimental and theoretical investigation focuses on film-drop-producing surface bubbles. Controlling fluid properties such as temperature, salinity and volatility, coupled with changes of ambient air saturation, we elucidate the ageing and lifetime of bubbles. We derive and validate a generalized bubble cap drainage model accounting for both curvature-pressure-induced drainage and Marangoni flows induced by the coupling between the bubble and its surrounding air. We show that this deterministic drainage is coupled with stochastic local perturbations, both intrinsic and extrinsic, from impacts by mist droplets to microbubbles. We derive the conditions for such perturbations to be lethal to the cap film, involving the competition of mixing and drainage time scales on the bubble, the film thickness, the size of the perturbation and the local Marangoni stresses introduced. We explain how the mixing dynamics on the cap ensures that bursts mostly occur at the foot of bubbles rather than on their cap. Our study sheds light on the coupling between the deterministic cap thinning and the stochastic events leading to bubble death. We conclude that ubiquitous water contaminants enable the birth of a bubble, sustain it through its ageing, but ultimately also kill it.
-
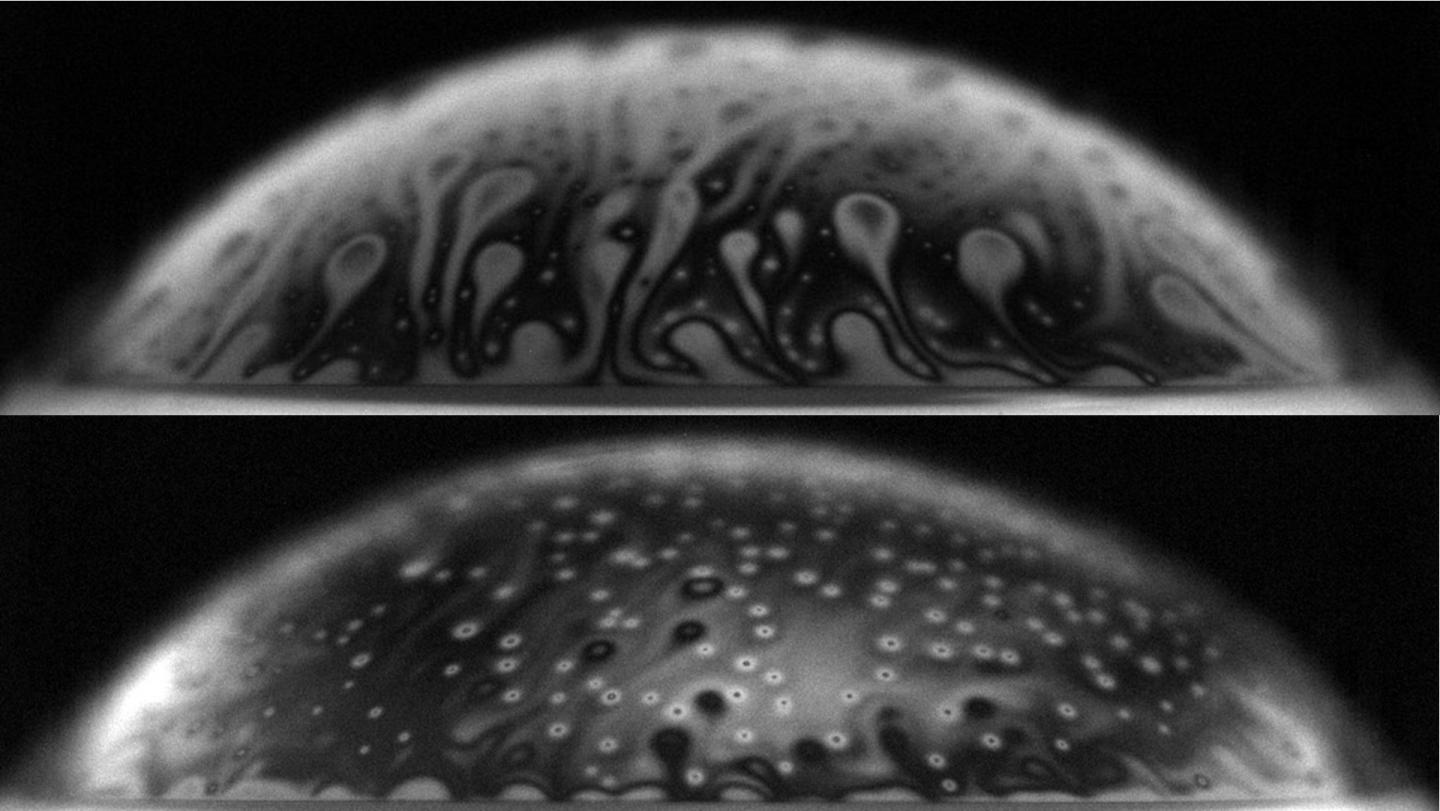Biosurfactants change the thinning of contaminated bubbles at bacteria-laden water interfacesStéphane Poulain, and Lydia BourouibaPhysical Review Letters, 2018Bubbles reside at the water surface before bursting, emitting droplets that can contain chemicals and pathogens linked to disease and contamination. We discover that bacterial secretions enhance the lifetime of bubbles. We also reveal and elucidate two distinct regimes of thinning for such contaminated bubbles. Initially, marginal regeneration governs their thinning rate, similarly to clean water bubbles. However, due to their enhanced lifetime, it is eventually evaporation that governs their thinning, thus also dramatically decreasing their thickness at burst. We derive and experimentally validate the expression for the critical timescale at which the transition between the two regimes occurs. The shift in thinning law makes the droplets produced by contaminated bubbles smaller, faster, and more numerous than those produced by clean bubbles. Our findings suggest that microorganisms can manipulate the aging physics of surface bubbles to enhance their own water-to-air dispersal.
2015
-
Particle motion induced by bubble cavitationStéphane Poulain, Gabriel Guenoun , Sean Gart , William Crowe , and Sunghwan JungPhysical Review Letters, 2015Cavitation bubbles induce impulsive forces on surrounding substrates, particles, or surfaces. Even though cavitation is a traditional topic in fluid mechanics, current understanding and studies do not capture the effect of cavitation on suspended objects in fluids. In the present work, the dynamics of a spherical particle due to a cavitation bubble is experimentally characterized and compared with an analytical model. Three phases are observed: the growth of the bubble where the particle is pushed away, its collapse where the particle approaches the bubble, and a longer time scale postcollapse where the particle continues to move toward the collapsed bubble. The particle motion in the longer time scale presumably results from the asymmetric cavitation evolution at an earlier time. Our theory considering the asymmetric bubble dynamics shows that the particle velocity strongly depends on the distance from the bubble as an inverse-fourth-power law, which is in good agreement with our experimentation. This study sheds light on how small free particles respond to cavitation bubbles in fluids.
